計算生物學聊聊：Hidden Markov Chain (上)

Last updated on Jan 12, 2025 7 min read 計算生物學

Quick look

Hidden Markov Chain(HMM)是計算生物學中一個重要的數學模型，廣泛應用於DNA序列分析和蛋白質結構預測等領域。HMM的核心概念是用隱藏的狀態來建立模型，並解釋觀察到的數據，通過轉移機率和觀察機率來描述系統的動態行為。

Markov chain

Markov chain是一種數學模型，用於描述一個系統在離散時間內的狀態轉移過程。它的核心特點是 "無記憶性"，即下一個狀態僅取決於當前狀態，而與過去的狀態無關。

基本定義

Markov chain 的所有可能狀態的集合，通常表示為：

$$ S={s1,s2,…,sn} $$

轉移概率（Transition Probability）

從當前狀態Si 到下一個狀態Sj，記為Pij:

$$ Pij=P(Xt+1=Sj∣Xt=Si) $$

其中，Xt 表示時間t 時系統的狀態

轉移矩陣（Transition Matrix）

$$ P = \begin{bmatrix} P_{11} & P_{12} & \ldots & P_{1n} \\ P_{21} & P_{22} & \ldots & P_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ P_{n1} & P_{n2} & \ldots & P_{nn} \end{bmatrix} $$

每一列的概率總和為 1：

$$ \sum_{j}Pij=1 $$

初始分佈（Initial Distribution）

系統初始時處於每個狀態的概率，記為向量 π:

$$ π=[π_1,π_2,…,π_n],\sum_{i=1}π_i=1 $$

Markov chain的性質

無記憶性（Markov Property）

下一狀態的分佈僅取決於當前狀態：

$$ P(Xt+1=Sj∣Xt=Si,Xt−1,…,X1)=P(Xt+1=Sj∣Xt=Si) $$

穩態分佈（Stationary Distribution）

當Markov chain運行足夠長時間後，系統的狀態分佈趨於穩定，滿足：

$$ π = πP $$

Markov chain 實例

假設我們有一個系統，代表每天的天氣狀態，狀態空間為：

$$ S = [晴天, 雨天] $$

轉移概率如下：

晴天後下一天仍是晴天的概率為 0.8; 變為雨天的概率為 0.2。
雨天後下一天變為晴天的概率為 0.6，仍是雨天的概率為 0.4。

轉移矩陣可以表示為：

$$ P = \begin{bmatrix} 0.8 & 0.2 \\ 0.6 & 0.4 \end{bmatrix} $$

初始分佈：

假設第一天是晴天：

$$ π=[1,0] $$

運行Markov chain可以計算未來任一天的天氣分佈。

HMM

HMM常用於分析序列數據或時序數據，尤其是當觀察數據（顯性數據）與內部狀態（隱藏狀態）之間存在間接關係時。HMM 是一種生成式模型 (generative model)，通過隱藏狀態的轉移和觀察狀態的生成來描述數據行為。

類似於Markov chain，HMM除了有觀察狀態之外，還包含了隱藏狀態 (hidden state)，隱藏狀態是一組未直接觀察到的狀態，用來描述系統的內部狀態。如投擲硬幣時，我們只會觀察到正面和反面，但是硬幣是真硬幣還是假硬幣是被隱藏起來的，而隱藏狀態之間的轉移由轉移機率矩陣來描述。而隱藏狀態生成觀察狀態的機率用觀察機率矩陣 (emission probability matrix) 來描述：

$$ B={b_jk},b_jk=P(ok∣Sj) $$

HMM 性質

隱藏狀態與觀察數據的關係隱藏狀態 S 影響觀察數據 O，但隱藏狀態本身無法直接觀測。每一個觀察 Ot 僅與當前隱藏狀態 St 相關。
隱藏狀態之間的轉移滿足Markov chain property，未來的狀態僅依賴當前狀態，與過去狀態無關。

範例

接下來我來看一個簡單的例子：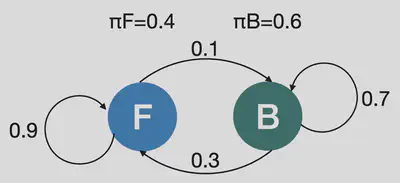

這張圖是一個兩狀態HMM，其中隱藏狀態代表公平硬幣（Fair Coin, F) 與偏斜硬幣（Biased Coin, B)，並包含以下數學定義：

初始狀態分佈:

$$ πF=0.4,πB=0.6 $$

這表示系統初始時處於公平硬幣狀態的機率為 0.4，而偏斜硬幣狀態的機率為 0.6。

轉移機率矩陣 (隱藏狀態的轉移機率):

$$ A = \begin{bmatrix} P(F \to F) & P(F \to B) \\ P(B \to F) & P(B \to B) \end{bmatrix} = \begin{bmatrix} 0.9 & 0.1 \\ 0.3 & 0.7 \end{bmatrix} $$

觀察機率矩陣:

每個隱藏狀態對應不同的觀察機率分佈。

$$ B = \begin{bmatrix} P(H \mid F) & P(T \mid F) \\ P(H \mid B) & P(T \mid B) \end{bmatrix} = \begin{bmatrix} 0.5 & 0.5 \\ 0.8 & 0.2 \end{bmatrix} $$

上面的數學描述基本上告訴我們:

當處於某一隱藏狀態 St 時，根據對應的觀察機率矩陣 B 生成觀察 Ot。例如：

若 St = F，則生成 H 或 T 的機率皆為0.5。
若 St = B，則生成 H 的機率為0.8，生成 T 的機率為0.2。
機率計算對於給定的觀察序列O = {H, T, H}，我們可以計算總機率：

$$ P(O∣λ) $$

然而，上面的總機率必須考慮所有隱藏狀態的序列，即便是 H，有可能 fair coin或是biased coin擲出，而這兩種狀態都必須考慮進來，然後加總。所以一旦序列很長，計算的複雜度會變得很大，導致在計算上無法順利執行，為了解決個問題，接下來會介紹一些常見的HMM演算法來解決這個問題。

Forward procedure

前向算法（Forward Algorithm） 是 HMM 中用於計算觀察序列的總機率 P(O∣λ) 的一種高效動態規劃方法。這個機率表示給定模型參數 λ = (F,B,π) 時，生成觀察序列 O= {o1,o2,…,oT} 的機率。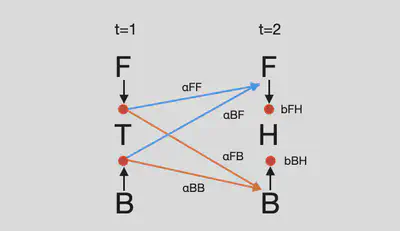

如圖二所示，我今天要來計算硬幣投擲序列的總機率，對於HMM來說，當下的隱藏態具有Markov chain property，亦即只依賴前一個隱藏態的分佈與轉移。

當t=1時，我們看到觀測值為 T，而T的出現機率由初始的隱藏狀態F和B來決定，而F與B分別有一個emission probability，表示由隱藏態映射到觀察值的機率，所以如果一開始投擲硬幣時使用到fair coin的機率為0.6，而使用此硬幣，也就是此狀態投出 T 的機率為0.5，那麼出現 T 的機率為 α1(F) = 0.6 * 0.5 = 0.3。

但是這還不夠，因為我們必須要考慮所有可能出現的狀態，因此還要考慮biased coin投擲時的情況，如果在biased coin 投擲下出現 T 機率為0.4 * 0.2 = 0.08，那麼在 t=1 時出現 T 的機率就等於 α1(B) = 0.3 + 0.08 = 0.38。

我們可以把兩個隱藏狀態映射出來的機率結果當成一個節點 （圖二中紅色的點），而這個節點儲存了隱藏狀態運算的結果，而我們可以把個運算結果傳到下一個觀察時間點，也就是下一次的投擲。

而這邊有一個很重要的概念就是，下一個觀察值取決於當下的隱藏狀態，而當下的隱藏狀態取決於前一個隱藏態，而非觀察值的結果，因為觀察值是已知，不像隱藏狀態有機率分佈，在了解了這個區別之後，接下來我們要進行下一次的硬幣投擲。第二次投擲的結果為H，所以累積到第二次投擲，O = {T, H} 的機率為以下所有情況的加總：

前一個狀態為 F，這次狀態為 F: α1(F) * αFF * bFH
前一個狀態為 B，這次狀態為 F: α1(B) * αBF * bFH
前一個狀態為 F，這次狀態為 B: α1(F) * αFB * bBH
前一個狀態為 B，這次狀態為 B: α1(B) * αBB * bBH

注意α1(F)及α1(B)已經記憶了前一個狀態的結果，所以再往後的運算，更前面的數據結果都可以拋棄，節省記憶體。

上面的過程可以用以下的數學式來描述：

初始化：對於時間 t=1：

$$ α_1(i) =π_i \cdot b_i(O_1),1≤i≤N $$

其中，πi 是初始狀態分佈，bi(O1) 是狀態 si 下產生觀察 O1 的機率。

遞推（時間 t>1）: 對於每個時間步t = 2,3,4,5…T，計算每個隱藏狀態的 αt(i)：

$$ \alpha_t(i) = \left( \sum_{j=1}^N \alpha_{t-1}(j) \cdot a_{ji} \right) \cdot b_i(o_t), \quad 1 \leq i \leq N $$

其中，

αt-1(j): 表示前一個時刻在狀態 sj 的機率。
αji: 表示從狀態 sj 轉移到 si 的機率。
bi(Ot): 表示在狀態 si 下生成觀察 Ot 的機率。

用上面的例子來說明，

αt-1(j) 為 α1(F): 表示前一個狀態為fair coin下的機率結果=0.3。
aji 為 αFF 及 αBF。
bi(Ot) 為 bFH 及 bBH。

結論

HMM 是在 Markov chain 上的擴展，允許狀態是隱藏的（hidden），而我們只能觀察到通過這些狀態生成的觀察值。它由三個主要部分構成：

隱藏狀態（Hidden States）：如公平硬幣（Fair Coin）或偏斜硬幣（Biased Coin）。
轉移機率（Transition Probabilities）：描述隱藏狀態之間的轉移。
觀察機率（Emission Probabilities）：描述隱藏狀態生成觀察值的可能性。

之後的文章我會探討針對其他演算法及HMM在生物資訊學中的運用。

Computational Biology Data Science