數據科學技術盤點:主成分分析?

Quick look
主成分分析(Principal component analysis, PCA)是一種強大且直觀的數據降維技術,被廣泛應用於臨床研究與醫學數據分析中。作為醫師,在日常工作中,我們經常面對大量的病患數據,例如基因表達數據、影像數據、實驗室檢驗值等。PCA能夠幫助我們提取數據的關鍵特徵,將高維度的資料轉換成易於解釋的低維度數據,從而揭示潛在的生物學意義。
主成分分析的數學基礎
核心思想
PCA的目的是將高維數據投影到一組新的互相正交的坐標軸上(稱為主成分),這些軸的排列方式使得:
- 第一個主成分最大程度地捕捉數據的變異性;
- 第二個主成分捕捉剩餘變異性,且與第一主成分正交,依此類推。
也就是在一堆雜亂的數據中,找到變異程度最大的主軸來最大程度的代表這群資料,接著PCA會逐步找到與這些主軸正交的其他軸,這些軸共同構成一組新的坐標系。而所有原始數據的值都會重新投影到新的軸上。每個空間中的數據點可以被所有主成分線性加成的方式來還原原始數據。整個過程可以大致簡化成如下的公式:
PCA的目的
我自己在分析基因數據的時候也很常用到PCA,甚至有些R bioconductor package也將PCA當成是標準前處理過程,但其實一開始都會思考,目前有其他降維工具,為何PCA還是很多人用?關於PCA的目的,初略有以下三點:
- 利用降維,去除高關聯性多餘的維度
- 利用視覺化在2維的座標上,發現離群值或異常值
- 跟隨最大離散程度的軸向,保留原始訊息
由此可見,PCA可以幫助在目前動則維度數百的資料集中,還能用視覺化分析主要數據,並且評估哪些特徵維度不具有分群的效果,而可以考慮刪除或用其他方式過濾。
數學過程
整個過程概念是先找到空間中數據點的平均值x-mean,即數據的中心點,然後以x-mean為原點,尋找通過此點的一個方向向量e,對於所有數據點xi,計算他們相對於x-mean的差值,並將這些差值投影到方向e上,在e方向上的投影值的總變異性(即投影值平方的總和)如果達到最大值,則e為第一主成分。 這邊的e為長度為1的單位向量,也就是需要經過正規化(normalization)處理,此單位化向量確保了比較不同方向時,投影的變異性(方差)完全由數據本身決定,而非向量的長度。
所有數據點投影後的長度可以表達為:
而在e上的數據變異度為:
接下來把上面的公式拆開: 平方公式可以看成兩個相同的元素相乘。
然而拆開為兩個矩陣,若要達到可以相乘的目的,後面的矩陣我們需要將其轉置。這邊我們回憶一下: $$ (AB)^T=B^TA^T $$ 所以上面的公式可以變換成:
接下來我們要找到離散程度最大值出現的方向e1: $$ e_1 = \arg\max_{e} e^T \Sigma e, \quad e^T e = 1 $$
這個算式若要求解,需要利用Lagrange function來針對約束條件來優化: $$ f(e, \lambda) = e^T \Sigma e + \lambda (1 - e^T e) $$ 分別對參數進行偏微分後,得到: $$ \frac{\partial f}{\partial e} = 2\Sigma e - 2\lambda e = 0 \implies \Sigma e = \lambda e $$ 及 $$ \frac{\partial f}{\partial \lambda} = 1 - e^T e = 0 \implies e^T e = 1 $$
到此,線代魔王eigenvalue現身了,搞了那麼久,PCA原來是要我們解eigenvalue problem!! 而不要忘記了,針對對稱矩陣,eigenvalue都有實數解,所以這邊必定能找到eigenvector,也就是eigenvalue對應的方向向量。 接下來我們只要做簡單的移項,就不難發現,我們要求解最大離散程度的e1,就是eigenvalue最大值的地方! $$ \lambda = e^T \Sigma e $$ 而第二主軸也可以依據Lagrange function來求解,但解完偏微分之後會發現,不管是接下來的哪個次主軸,解的都是跟原來的公式一模一樣,所以我們只要求第二大的eigenvalue以及其對應的相向即可!
實際運用
古人云:千言萬語不如一行code,我們來直接用R來玩玩看PCA是怎麼達成並且視覺化的。
#加載數據
set.seed(123)
data <- matrix(rnorm(100 * 3, mean = 5, sd = 2), ncol = 3)
colnames(data) <- c("Feature1", "Feature2", "Feature3")
#標準化數據,將數據移到中心
scaled_data <- scale(data, center = TRUE, scale = TRUE)
#計算共變異矩陣
cov_matrix <- cov(scaled_data)
#計算共變異矩陣的特徵值和特徵向量
eigen_result <- eigen(cov_matrix)
eigenvalues <- eigen_result$values
出來的eigen vectors:
| [,1] | [,2] | [,3] | |
|---|---|---|---|
| [1,] | 0.6733474 | -0.1690336 | 0.7197436 |
| [2,] | -0.3533758 | -0.9286934 | 0.1124905 |
| [3,] | -0.6494065 | 0.3300852 | 0.6850657 |
而eigenvalues: [1] 1.1505778 [2] 0.9801158 [3] 0.8693063
此時我們試著使用R中的prcomp來直接操作PCA:
#使用prcomp進行 PCA
pca_result <- prcomp(data, center = TRUE, scale. = TRUE)
接著來同樣取出eigenvalues,看看是不是跟上面的一樣
#取出eigenvalues prcomp用奇異值來解PCA,奇異值的平方就等於特徵值
prcomp_eigenvalues <- pca_result$sdev^2
prcomp_eigenvalues
出來的eigenvalues: [1] 1.1505778 [2] 0.9801158 [3] 0.8693063 跟上面操作的方式結果一至!
PCA的視覺化
接者我可以簡單的用ggfortify套件來查看PCA的結果。
library(ggfortify)
autoplot(pca_result, data = as.data.frame(data), colour = 'Feature1') +
ggtitle("PCA Projection") +
theme_minimal()
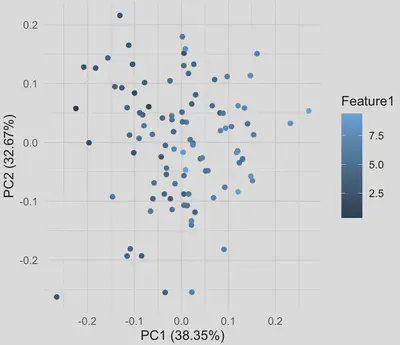
因為這個數據是隨機的,如果使用癌症基因數據,搭配一些顯著的臨床因子,視覺化後的分群應該會更漂亮。
結論
主成分分析是一項將複雜數據轉化為清晰結構的強大工具,就像一個數據的解碼器,幫助我們從看似混亂的數據中提煉出最重要的線索。透過數學的魔力,我們不僅能找到數據中最大變異的方向,還能有效地降維並視覺化,讓原本高維的「迷霧森林」變成清晰的「航路圖」。
在實際應用中,PCA不僅僅是一個數學公式,更是一種數據理解的思維方式。無論是在基因表達分析、醫學影像數據,還是多維臨床檢驗指標的綜合解讀中,PCA都能扮演一個「數據導航員」的角色,引領我們找到關鍵特徵,解決臨床問題,甚至發現潛在的生物學機制。
當然PCA也有其缺點:
- 解釋性不足: PCA的主成分是數學上計算出的線性組合,雖然能有效地捕捉數據的變異性,但每個主成分的實際意義通常不直觀,難以直接對應到具體的物理或生物學意義。例如,在醫學數據中,第一主成分可能代表數個臨床指標的綜合作用,但無法具體指出是哪一個指標在起主導作用。
- 假設數據線性: PCA基於線性代數方法,假設數據之間的關係是線性的。然而,在很多實際問題中(如基因調控網絡、非線性動力學模型等),數據之間的關係可能是高度非線性的,這會導致PCA無法有效捕捉數據的真實結構。
- 對數據尺度敏感: 如果數據的尺度(scale)差異很大,PCA的結果會嚴重受到影響。例如,一個變數的數值範圍是0-1,而另一個變數範圍是1-1000,後者會在主成分計算中占據主導地位。因此,PCA通常需要在降維前對數據進行標準化(Standardization),否則結果可能不準確。
- 對離群值敏感: PCA對於數據中的離群值(outliers)非常敏感,這是因為離群值會極大地影響共變異矩陣的計算,進而改變主成分的方向。如果數據中存在明顯的離群值,PCA的結果可能會失真,導致降維效果變差。
- 無法處理稀疏性問題: 在處理高維度但稀疏的數據(如基因表達數據或文本數據)時,PCA可能不是最佳選擇。這是因為PCA的降維過程會壓縮所有特徵的信息,導致稀疏結構丟失,無法保留某些特徵的稀疏性。
- 依賴均值與共變異: PCA基於數據的均值和共變異矩陣,假設數據的主要信息可以用這些統計量來描述。如果數據的分佈偏離高斯分佈或共變異矩陣無法很好地捕捉數據結構,PCA的效果可能會受到限制。
- 僅考慮變異性,無法考慮分類信息: PCA僅最大化數據的變異性,並不考慮下游任務(如分類或聚類)的需求。因此,如果主要目的是分類或分群,PCA降維後的特徵可能無法有效提高模型的性能。
在實際使用時,需要結合數據特性、應用場景以及模型需求,選擇適合的降維方法,必要時可考慮其他技術(如t-SNE、UMAP或LDA)作為替代或輔助方法。