計算生物學聊聊:分子表示法與圖神經網路

Quick look
分子表示法(molecular representation)在計算化學中扮演重要的角色,它使化學家和數據科學家能夠將複雜的化學結構轉換成機器可理解的形式,用於數據存儲和計算分析。這些表示法在格式、易用性和應用場景上存在顯著的差異,每種表示法在特定類型的分析中具有其獨特的優勢和局限性,透過建構圖神經網路(Graph neural network, GNN)來預測分子的特性,這些表示法的差異會更為顯著。
本篇筆記出自於美國麻省理工學院的計算生物學課程MLCB24。課程影片請看這裡。
常見的分子表示法
SMILES (簡化分子輸入線性表示系統)SMARTS(SMILES 任意目標規範)InChI(國際化學標識符)Molecular graph (分子圖)
接下來會根據每一種表示法做介紹:
SMILES
SMILES(Simplified Molecular Input Line Entry System)是一種基於字串的分子表示法,最初由美國環保署(EPA)開發,用於以緊密相連的線性格式捕捉分子的結構。目前為化學資訊學中最廣泛使用的小分子表示法之一。
格式
例如,乙醇的 SMILES 表示為 CCO(省略氫原子)。字母和數字表示原子與鍵類型(單鍵、雙鍵等),括號則用來標示分支結構。
優點
SMILES 具有高度壓縮性(compact),容易被大多數化學資訊軟體讀取,適合用於資料庫存儲。
限制
合成混淆:SMILES 字串靈活性高,容易生成,但這種靈活性導致許多語法有效的 SMILES 字串可能無法解碼成實際分子。
立體化學:雖然 SMILES 可以包含立體化學資訊,但通常在實務上會被省略,當分子功能取決於立體資訊時,會導致問題產生。
SMARTS(SMILES 任意目標規範)
SMARTS 是根據 SMILES 來擴展的表示法,允許在 SMILES 字串中進行模式匹配來識別特定的分子子結構。
應用
SMARTS 對於化學資訊學中的子結構搜索特別有用,例如識別芳香環或其他分子功能基團。
格式
例如,芳香環可以用c1cccccc1來表示。
限制
儘管 SMARTS 在子結構搜索中功能強大,但比 SMILES 更複雜,需要對化學模式有更深入的理解才能有效使用。
SELFIES(自引用嵌入字串)
SELFIES 是一種較新的表示法,主要在克服 SMILES 的一些限制。它更像是一種分子編程語言,允許完整解構字串,系統化生成分子,
關鍵優勢
可以很好的耐受錯誤,所有的SELFIES字串都可以解構成某特定分子,不會導致訊息的喪失,有利於機器學習。
格式
例如,苯環可以表示成:C1=CC=CC=C1。
限制
SELFIES 雖然創新,但較難閱讀,且需進一步改進以確保化學空間中的採樣沒有偏誤。
InChI(國際化學標識符)
InChI 是一種IUPAC開發的標準化分子表示法,保證每個分子與其 InChI 字串一一對應。包含多層的分子特徵,如連結性、價電子、空間化學與異構物等。
應用
InChI 在資料庫搜索和比較中特別有價值,因為它允許直接進行分子比較,避免了因不同 SMILES 表示法導致的多餘訊息。因為SMILE並沒有賦予分子獨特性,因此需要電腦解讀,增加計算負擔。
關鍵優勢
標準化的表示法,每一個表示法都對應到單一獨特的分子式。
格式
例如,乙醇可以表示成:1S/C2H6)/c1-2-3/h3H,2H2,1H3。
限制
InChI 的複雜性使其難以閱讀和解釋。由於簡潔性,許多人更偏好用 SMILES 進行可視化。目前有方法將SMILES表達法InChI化,藉此增加InChI的可讀性。
分子圖
分子圖是一種基於圖形的分子表示法,其中原子是頂點,鍵是邊。這種表示法捕捉了分子的所有信息,包括原子類型、鍵類型,甚至是立體化學。
優點
分子圖全面地提供分子結構的完整描述,較為直覺,尤其適用於基於圖的機器學習中的計算分析。
限制
與基於字串的格式不同,分子圖不如 SMILES 那麼緊密,也不適合快速搜索資料庫。分子圖更適合用於計算應用和視覺化,而非數據儲存。
分子表示法比較
圖一顯示不同分子表示法的總結。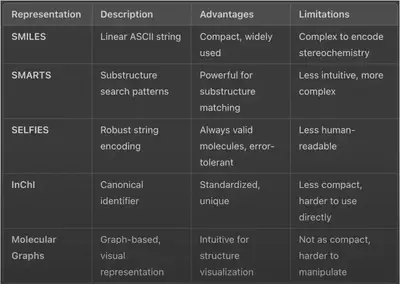
SMILES 表示法
原子與鍵
一般原子:在 SMILES 字串中,每個原子由其化學符號表示。大多數原子使用單個大寫字母表示(例如,C 表示碳,O 表示氧)。一些原子需要兩個字母的組合(如Na 表示鈉,Cl 表示氯)。芳香原子:在 SMILES 中,小寫字母表示芳香化合物中的原子。例如,小寫的 c 表示芳香碳,常見於苯環中。鍵:單鍵通常為簡化省略,但也可使用單個破折號-明確表示。雙鍵用等號=表示,三鍵用井號#表示。芳香鍵通常省略,因為小寫原子符號已隱含芳香性。分子組件的分離:句點.用於表示分子中不連接的部分,例如鹽或離子對。例:Na.Cl 表示氯化鈉。
鏈與分支
線性鏈:簡單的原子鏈以直線順序表示。例如,乙醇的 SMILES 表示為 CCO,表示碳-碳-氧鏈。分支:SMILES 使用括號表示從主鏈分支的結構。主鏈從括號前的原子開始繼續。例如,異丙醇 (2-propanol or isopropanol)的 SMILES 表示為CC(O)C,其中(O)表示OH-分支。
其他例子:
CC(=O)C: 2-Propanone
CC(CC)C: 2_Methylbutane
CC(C)CC(=O): 2-Methylbutanal
c1c(N)(=O)=O)cccc1: Nitrobenzene
CC(C)(C)CC: 2,2-Dimethylbutane
環與環狀結構
環閉合:SMILES 使用數字標記環閉合。例如,苯的表示為c1ccccc1,其中1表示第一和最後的碳原子相連以完成環。相同的數字表示開環與閉環的原子位置。鍵的類型著記在原子之後,但在數字之前。多重環:對於更複雜的環系統,使用額外的數字來表示分子內的每個環。例如,萘的 SMILES 表示為 c1ccc2ccccc2c1,其中 1 和 2 標記了兩個融合的環 (圖二)。
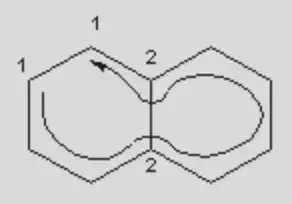
電荷
電荷表示:SMILES 使用卷曲括號 {} 和加號 + 或減號 - 表示原子的電荷。
模稜兩可的名稱
若是比較容易讓人誤解的標示方法,用大括號 [] 來區分,如Sc沒有框起來的話表示Sulfur與aromatic carbon,而[Sc]則表示Scandium。
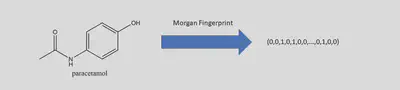
Morgan 指紋:機器學習中的分子結構編碼
Morgan 指紋(也稱為環狀指紋)是一種強大的工具,可將分子結構轉換為固定長度的二進制向量,使其非常適合於機器學習應用。與需要詳細結構數據的完整分子圖不同,Morgan 指紋提供了一種計算效率更高的表示方式,捕捉每個原子周圍的結構特徵並以易於輸入機器學習模型的格式儲存。
Morgan 指紋的目的
定量結構-活性關係(QSAR)建模:例如,預測分子的疏水性、溶解度或潛在生物活性。高通量篩選:在藥物發現中,用於快速篩選分子。
主要優勢
固定長度表示:每個分子無論大小都表示為特定長度的向量,與許多機器學習模型直接兼容。結構資訊封裝:通過編碼以原子為中心的子結構(達到指定半徑),捕捉局部化學環境。計算效率:這種表示方式比生成完整分子圖更快,並且生成的指紋可快速用於機器學習。
Morgan 如何運作?
生成 Morgan 指紋涉及一系列步驟,這些步驟專注於分子中的每個原子,並檢查其在指定半徑內的局部結構 (圖三)。
以原子為中心的編碼: 每個原子作為中心點,檢查其周圍的子結構。這些子結構的細節取決於設定的半徑。
定義半徑:
半徑 0:僅編碼原子本身。
半徑 1:編碼原子及其鄰近原子。
半徑 2:編碼原子、其鄰近原子及這些鄰近原子的鄰居。
通常,使用半徑 2 即可捕捉足夠的細節,而不會導致向量過於龐大。
將子結構映射到比特 (bit) 位置:每個環狀子結構都被編碼為一個二進制向量(bit string),其中特定特徵(例如原子、鍵、環)的存在記錄為1,缺失記錄為0。半徑決定了圍繞中心原子的原子層數(例如,半徑為2時包括距離中心原子兩鍵以內的原子和鍵)。子結構碰撞:子結構被哈希(hash)轉換為固定長度的指紋(例如1024位),這可能導致哈希碰撞,即多個子結構可能映射到相同的位。可以考慮增加長度來解決。
Morgan 指紋生成範例
- 第一步:從分子內的某原子開始。
- 第二步:根據特定的半徑來建構子結構。
- 第三步:使用Hash table來將子結構轉換成獨特的比特編號。
- 第四步:針對每一個原子完成以上步驟,產生一個二元分子指紋,表示整個分子。
以乙醇(CCO)為例
每個碳和氧原子作為中心點,評估其半徑 2 內的子結構。
這將產生以下信息:
- 原子 1:第一個碳及其鄰居(第二個碳和氧)。
- 原子 2:第二個碳及其鄰居(第一個碳和氧)。
- 原子 3:氧及其鄰近的碳。 每個原子和子結構會映射到指紋中,形成唯一表示乙醇結構的比特向量。
Morgan 指紋的優點
- 對結構改變非常敏感,結構的些微修飾都可以被捕捉。
- 效率高。
- 廣泛使用於常見化學資訊學的工具中,如
RDKit,也常用在視覺篩選與相似性搜索中。
半徑與比特向量長度的平衡
半徑增加的影響:
- 半徑越大,捕捉的子結構越詳細,但需要更大的向量以避免碰撞。
- 半徑 2 提供了適度的細節,廣泛用於化學資訊學。
- 半徑 3 或更大通常僅在需要非常細粒度結構細節時使用,但會顯著增加計算需求和複雜性。
向量長度
常用長度為 1024 或 2048 比特。更大的向量幫助減少哈希碰撞,但在數據集較小時可能導致稀疏性問題。
在機器學習中的解釋與應用
Morgan 指紋將複雜的分子結構轉換為向量空間表示,其中具有相似拓撲特徵的分子具有相似的指紋。結果向量可用於以下機器學習模型:
隨機森林:適合特徵豐富的數據集,向量直接表示分子特徵。多層感知機(MLP):能有效處理 Morgan 指紋,學習數據中的非線性模式。- 其他演算法:包括支持向量機(SVM)和邏輯回歸在內的任何處理二進制或數值向量的演算法均可使用 Morgan 指紋。
限制與考量
不可逆:指紋無法反向解碼為原始分子。- 碰撞問題:不同的分子結構可能映射到相同的比特位置,尤其是在
較小的比特向量或大分子時。 - 不適用於大生物分子:對於
非常大的生物分子(如蛋白質),Morgan 指紋可能不適用,因為結構的複雜性超出了其表達能力。
分子圖:化學結構的進階表示
分子圖是一種靈活且精細的方式,能夠以數學形式表示分子,特別是在指紋無法捕捉足夠結構細節時尤其有用。與比特向量指紋不同,分子圖提供了分子結構的直接映射,將每個原子作為節點 (node),每條鍵作為邊 (edge)。這種基於結構的表示允許更高的特異性和數據的豐富性,使其成為圖神經網絡(Graph Neural Networks, GNNs)的最佳輸入,尤其適用於需要深入探索原子間的關係時,例如定量QSAR和藥物設計。
分子圖的結構
節點與邊:在分子圖中,每個節點表示一個原子,每條邊表示一條化學鍵。這種結構捕捉了分子內的原子類型及鍵類型(單鍵、雙鍵、三鍵或芳香鍵),能夠詳細描述化學關係。節點標籤:每個節點可以攜帶標籤或類型(例如,碳用 C 表示,氮用 N 表示),以區分不同的原子類型。邊標籤:邊可以標示鍵的類型(如單鍵、雙鍵、三鍵等)。這在分子圖中尤為重要,因為鍵類型對分子的化學行為和特性有著重要影響。
圖的種類
方向性:在大多數情況下,分子圖是無向 (undirected)的,因為化學鍵通常沒有方向性。但在某些情境下,如化學反應網絡中,可以使用有向圖 (directed)來表示從反應物到產物的轉化流程。圖標籤:原子和鍵都被標示,說明原子和鍵的類型,在對於需要化學分子細節的探討中很重要。加權圖:雖然在基本分子圖中不常使用,但可以引入加權邊以指示鍵強度、相互作用強度或其他結構行為的先驗知識。對稱性:對於無向圖,鄰接矩陣是對稱的;對於有向圖,則是非對稱的,反映每條邊的方向性。
分子圖的表示方法
鄰接矩陣 (Adjacency Matrix):
鄰接矩陣提供了一種表格式的圖表示,其中每個單元格表示原子之間是否存在鍵(或鍵的類型)。例如,若原子
(i,j) 的值為 1(或表示鍵類型的整數);否則為 0。
鄰接列表 (Adjacency List)
在處理大型圖(如社交網絡或大規模數據集)時比矩陣更高效。每個原子只保存與其直接相連的原子清單,大大減少稀疏網絡中的存儲需求。
稀疏矩陣表示:
另一種選擇是使用稀疏矩陣,只存儲非零值(即存在鍵的原子對),進一步降低內存使用量。
圖的可視化:
分子圖也可以被可視化,提供直觀的方式來檢查分子結構、理解其複雜性並排查表示中的問題。
分子圖的應用與優勢
完整的結構編碼:分子圖保留了分子的完整拓撲結構,允許對其特性和相互作用進行更深入的檢查。
- 與圖神經網絡(GNNs)的兼容性:分子圖可以與 GNNs 無縫集成,後者專門設計用於處理圖結構數據。
- 強化的預測模型:基於分子圖構建的 GNN 模型能夠更準確地預測分子的各種特性,如生物活性、毒性、溶解度和結合親和力。
- 消息傳遞:在 GNN 中,每個節點通過一種稱為消息傳遞的迭代過程與其鄰居進行通信。這允許每個節點聚合鄰近節點的信息,有效地捕捉其分子環境的影響。
- 分層結構:與傳統神經網絡類似,GNN 有多層結構,每層允許圖捕捉分子中越來越遠的關係。
- 可定制性:GNN 可以納入方向性和邊權重的設計,特別適合於處理具有專門相互作用的分子結構。
其他圖應用
雖然分子圖是化學中的自然選擇,但其原則和技術可廣泛應用於其他與圖相關的領域,例如:
- 社交網絡:節點表示個體,邊表示聯繫(通常是有向的)。
- 通訊網絡:路由信息,其中節點表示服務器或路由器,邊表示數據流路徑。
- 生物網絡:基因與蛋白質的交互網絡,節點表示基因或蛋白質,邊表示相互作用或調控關係。
運用分子圖於藥物開發領域
分子圖在藥物發現和開發的各個階段都不可或缺,能夠精準捕捉並操作分子的完整結構。以下是分子圖如何顯著提升藥物開發流程的幾種方式:
化學相似性搜索 (Chemical similarity searching)
- 當一種化合物顯示出與特定靶點的良好結合親和力時,研究人員通常會尋找與之結構相似的化合物,因為它們可能具有類似的活性。通過分子圖,我們可以編碼已知化合物的結構特徵,並在包含數百萬化合物的大型化學庫中搜索類似結構。
- 研究人員可以優先選擇較小且更具針對性的分子集進行初步測試,從而減少大規模篩選的成本和資源使用。
定量結構-活性關係(QSAR)建模
- QSAR 模型使用分子圖來預測各種生物化學和藥代動力學特性。例如,可以基於分子結構預測以下屬性:
- 溶解度
- 血腦屏障的滲透性
- ADME(吸收、分布、代謝、排泄)
- 毒性
基於結構的藥物設計分子圖允許進行基於結構的藥物設計,通過表現完整的分子結構,支持更準確的分子-靶標作用模擬與預測。
- 研究人員可以利用基於分子圖的表示法來模擬
結合能量及交互動態,設計專門與目標結合的化合物。
卷積神經網絡 (CNNs)
為更直觀地理解GNNs,可以先考慮CNNs的結構與功能。
CNN 處理 2D 網格數據: 以像素為單位:CNN 將每個像素視為一個單位,並與相鄰像素進行連接(垂直或水平),從而學習局部模式(如邊緣、梯度和紋理)。層級學習:隨著網絡層數的增加,CNN 將這些初級特徵聚合為更高級模式,最終能夠識別複雜對象(例如貓、狗或汽車)。- 從 CNN 到
幾何深度學習(GDL)的過渡: 將 CNN 在結構化數據(如影像)上的成功推廣到非結構化、非歐幾里得數據,如圖和流形(graphs, meshes and point clouds)。
而圖與網格或矩陣不同,因其缺乏固定的節點排列且連接多樣化,因此需要專門的神經網絡架構,因此才有圖神經網路的角色出現。
Invariance 與 Equivariance
在深度學習中,Invariance(不變性)與 Equivariance(等變性)是兩個非常重要的概念,特別是在處理結構化數據(例如圖像、序列、圖)時,對模型的性能和泛化能力有著深遠的影響。
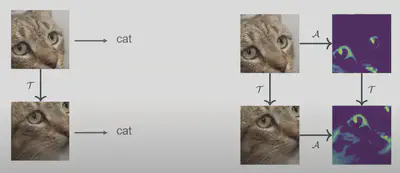
- Invariance: 不變性指的是模型或函數對某些輸入變換保持輸出不變的特性。如果f(x)是某個模型或函數,針對某個變換T,不變性表示:
如圖四,貓的圖片在轉換之後,模型仍然能偵測為貓。或是一個模型在預測分子溶解度時應該對分子的旋轉或平移保持不變,因為這些變換不影響分子的溶解性。
- Equivariance: 等變性指的是模型或函數對某些輸入變換的輸出也發生相應的變換。如果f(x)是某個模型或函數,針對某個變換T,等變性表示:
換句話說,輸入經過某種變化後,輸出的結果應該跟著同步變化。例如,分子動力學模擬中,對參考框架的旋轉應該導致原子位置與動量的相應旋轉。
圖神經網路
圖神經網絡是一類專為處理圖結構數據而設計的深度學習模型。與傳統神經網絡處理網格數據(如圖像或時間序列)不同,GNNs 專注於以節點(例如原子)和邊(例如化學鍵)表示的圖結構數據,這使其在分子圖、社交網絡和知識圖譜等複雜結構中應用廣泛。GNNs 的目標是捕捉圖中的關係與依賴性,預測與節點、邊甚至整個圖相關的特性或行為。
關鍵概念
圖神經網路可以學習如何表達以圖為結構的數據,並且可以利用節點和邊的關係來做預測。
GNN 的關鍵應用
廣泛使用於化學資訊學、生物資訊學與社群網路分析。
節點級預測:
- 應用:例如預測某特定節點(如分子中的原子)是否會參與活性位點的結合或參與化學反應。
- 實例:在蛋白質-小分子交互研究中,GNN 可預測分子中的
哪個原子參與結合位點。
邊級(鏈路)預測:
- 應用:判斷節點間邊的存在性或強度(例如化學鍵的形成可能性)。
- 實例:基因組學中,預測可能與疾病相關的基因之間的潛在關聯。
圖級預測:
- 應用:為整個圖進行分類或性質預測,例如預測
分子的毒性或是否能穿越血腦屏障。 - 實例:在藥物篩選中,基於
整個分子結構預測其生物活性。
GNN 的一般工作流程
GNN 的工作流程通常包括以下幾個階段:
輸入數據與初始嵌入: 圖中的每個節點都有一些初始輸入特徵。例如,在分子應用中,每個節點可能表示一個原子,其特徵可能包括原子序數、電荷狀態等。這些初始特徵被嵌入到一個高維空間中的潛在表示中(latent representation),以捕捉每個節點的初始狀態。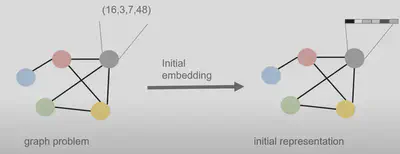
圖五 圖神經網路的節點特徵嵌入 通過 GNN 層進行
信息傳遞 (Message Passing): 嵌入後,GNN 在多層網絡中進行一系列的消息傳遞(message passing)步驟。這一過程類似於 CNN 中的卷積操作,CNN 是從鄰近像素中聚合信息,而 GNN 則是從相鄰節點中聚合信息。聚合與更新: 在每一層 GNN 中,每個節點都從其鄰居處接收訊息。節點將這些訊息聚合起來,與自身的潛在向量結合後
更新其狀態。這種聚合方法可以是求和(sum)、均值(mean)、或最大池化(max pooling),具體取決於任務需求。 以下是一些常見的聚合技術:總和聚合(Sum Aggregation):透過將所有節點的representation相加,我們可以獲得一個單一的向量,反映來自所有節點的累積信息。這種方法在節點數量在不同圖之間相近時效果不錯,但如果某些圖比其他圖大得多,可能會導致偏差。平均聚合(Mean Aggregation):通過對節點向量取平均值,這種方法在聚合過程中進行了歸一化,確保圖的大小(節點數量)不會影響結果。當處理大小不同的圖時,平均聚合特別有用,因為它可以調整節點數量之間的差異。最大池化(Max Pooling):在這種方法中,我們從所有節點向量的每個位置中取最大值,捕捉到最顯著的特徵值。這種方法能夠突出圖中最具代表性的特徵,但可能會忽略一些重要的細微特徵,特別是當其他節點包含較低但關鍵的值時。注意力機制(Attention Mechanisms):基於注意力機制的方法允許我們根據節點對任務的重要性,對每個節點的貢獻賦予不同的權重。模型會自動學習這些權重,從而自適應地突出關鍵節點,是一種強大的方法來優先考慮圖中的某些區域。例如,在分子圖中,注意力機制可以對重要的功能基團賦予更高的權重,以便在預測化學性質時更加精準。全局節點或虛擬節點(Global Nodes or Virtual Nodes):在一些進階的 GNN中,會引入一個全局節點或虛擬節點,該節點與圖中的所有其他節點相連。在信息傳遞(message-passing)過程中,這個節點會聚合來自整個圖的所有信息,作為一個中心樞紐。到最後,這個虛擬節點的潛在向量(latent vector)就成為整個圖的表示,捕捉了整個網絡的特徵。


節點的更新公式:
更新機制
Step 1: 每個節點先從鄰居中收集信息(聚合鄰居特徵)。
Step 2: 將聚合後的鄰居特徵與自身特徵結合(線性變換 + 偏置項)。
Step 3: 應用激活函數,生成該節點在新層的嵌入特徵。
多層結構: 信息通過
多層傳遞,每層使節點可以看到圖中更遠的鄰居。例如,經過兩層後,每個節點可以融入來自其兩跳鄰居的信息。最終狀態與輸出生成: 當圖經過多層 GNN 處理後,節點達到最終狀態,該狀態包含從周圍節點學到的信息。這些最終狀態可以用於生成多種預測:
節點級任務:使用每個節點的最終狀態進行預測。當我們需要為單個節點分類或預測屬性時,可以直接使用每個節點的最終潛在表示(latent representation)。例如,假設我們有一個分子圖,並且已知每個原子的分子屬性,但對某個特定原子(節點)缺乏相關信息,我們可以將該未知節點的潛在向量輸入分類器,來預測所需的屬性,例如該原子是否參與結合位點,或者是否與某些分子相互作用。邊級任務:分析相鄰節點最終狀態之間的關係。連結預測的目標是預測節點之間的連接(邊)的存在性或強度,這在社交網絡或生物網絡中非常有用,可以用來推斷新的關係。例如,在基因組學中,我們可能已知與某種疾病相關的一組基因,並希望通過檢查它們在生物途徑中的連接性,來預測其他潛在的基因。這可以通過以下方式實現:將兩個節點的潛在向量進行相似性測量(例如餘弦相似度)或學習函數,來預測是否存在一條邊。更複雜的情況下,將兩個節點的表示組合後輸入多層感知器(MLP),以進行關係的預測。圖級任務:將所有節點的最終狀態池化成單一圖表示,用於分類或回歸。在某些情況下,我們需要對整個圖進行單一的預測,例如分子的溶解度或毒性。這時需要將所有節點的信息聚合成一個固定長度的向量,該向量能夠捕捉整個圖的結構和特徵。例如:可以使用聚合技術(如平均聚合、總和聚合或注意力機制)來匯總節點的表示,生成代表整體圖特徵的向量。 然後,將該圖級表示作為輸入,用於進行分類或迴歸任務。
擴大感受野
每當我們應用一層 GNN層時,實際上我們就增加了每個節點的感受野 (receptive filed)。起初,一個節點的感受野僅包括它自己。然而,在第一層之後,該節點的表示(representation)將會結合來自其直接鄰居的信息。經過第二層後,該節點的表示將會包含來自兩跳 (K-hops=2) 鄰居(即鄰居的鄰居)的信息,依此類推。這種擴展意味著節點可以逐漸從圖中更大的區域累積信息。
例如,在分子圖中,一個碳原子的感受野起初可能僅包括直接鍵合的原子(例如一個相鄰的氧原子)。而經過兩層 GNN 層後,該碳原子可以結合來自兩個鍵距離的原子的信息,提供更多的化學訊息。
層數深度與信息擴散
雖然看似增加層數可以最大化節點的感受野,但更深的網絡層數也會帶來一些問題:
訊息稀釋(Information Dilution):隨著層數的增加,節點表示可能會過度混合(overly blended),失去原本的特徵,從而難以區分不同的節點。這種現象通常被稱為過平滑(oversmoothing),在處理複雜任務時可能導致性能下降。計算成本(Computational Costs):增加層數需要更多的計算資源,同時也會提高訓練過程中出現梯度消失或梯度爆炸問題的風險,從而使訓練變得更加困難。 因此,在許多實際應用中,使用有限層數的 GNN(例如 2-4 層)是更為有效的策略。這種方法在計算效率與每個節點能夠融合的信息深度之間取得了平衡。
GNN 層中的操作旨在將卷積操作推廣到圖結構,其中空間結構由節點之間的邊定義,而不是固定的空間坐標。
圖上的卷積(Convolution on Graphs):在 CNN 中,卷積在固定的網格上進行;而在 GNN 中,卷積基於每個節點的鄰域進行。這種局部特徵的聚合使得每個節點可以從其鄰居中學習,同時保留圖的固有結構。池化與讀出(Pooling and Readout): 與 CNN 中的池化層類似,GNN 的池化用於減少維度並聚合節點信息。池化可以應用於子圖內的節點,也可以應用於整個圖,用於生成圖級輸出。正規化(Normalization): 由於節點的度數(連接數)可能不同,對聚合的消息進行正規化有助於防止模型過度依賴於高連接節點,並保證信息流的平衡。
GNN 在分子建模與藥物發現中的優勢
GNN 的結構化消息傳遞使其能夠有效地從複雜的關係中學習,這在分子和生物應用中尤為重要。主要優勢包括:
- 靈活處理複雜結構: GNN 能夠處理分子圖的不規則和非歐幾里得結構,其中原子和鍵並不遵循網格狀結構。
- 高效利用結構信息: 通過嵌入和消息傳遞,GNN 能夠內在地尊重分子內的空間和化學關係。
- 可擴展性: GNN 通過基於鄰域的聚合機制,可以有效處理大型圖形數據,例如虛擬篩選中的分子庫。
結語
使用 GNN 的輸出需要考慮很多的因素,包括任務的性質、數據的結構,以及圖的大小和多樣性。在這個過程中,從聚合技術到模型類型的每一個選擇,都會影響 GNN 對於進行準確且具普遍性預測的能力。
通過調整這些步驟,並為每種類型的預測選擇合適的方法,GNN 能夠成為處理複雜數據集的強大工具,特別是在藥物發現、分子建模、社交網絡分析等領域中發揮重要作用。